
ADC(アナログ-デジタル変換器)で取得したデータは量子化されているため、基準電圧に対してのバイナリデータになります。
そのままでも使える場合もありますが、抵抗値や電圧を測定する場合は、計算で求める必要があります。
様々な状況がありますが、換算式を忘れてしまって毎回手計算で求めているのでここにまとめようと思います。
スポンサーリンク
測定回路と変数
解説する前に、抵抗値や電圧を求めるために使う回路と変数を提示しておきます。
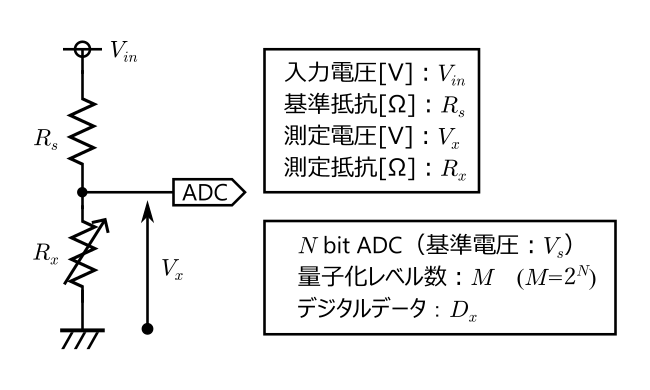
固定抵抗の![]() と可変抵抗の
と可変抵抗の![]() と書いていますが、これはいろんな状況があると思います。
と書いていますが、これはいろんな状況があると思います。
ボリュームであれば![]() と
と![]() のどちらも変化するでしょうし、どちらも固定で
のどちらも変化するでしょうし、どちらも固定で![]() が変化する場合もあります。
が変化する場合もあります。
基準電圧が![]() で
で![]() bitのADCを使います。
bitのADCを使います。
次項からの具体的な例は分かりやすいように Arduino Uno を使った場合で解説していきます。
その Arduino Uno でしたら10bit(![]() )のADCで、基準電圧
)のADCで、基準電圧![]() はデフォルトでは5Vです。
はデフォルトでは5Vです。
![]() が分かったので
が分かったので![]() となり、量子化レベル数
となり、量子化レベル数![]() は1024です。
は1024です。
ということはデジタルデータ![]() (analogReadで取得する値)は0~1023の値を取るはずです。
(analogReadで取得する値)は0~1023の値を取るはずです。
抵抗(Rx)にかかっている電圧(Vx)を求める
導出
これを求めるのが一番簡単です。
というのも、ADCは入力端子とGND間にかかっている電圧を見ていますからね。
他に紹介する回路はこの計算を必ずしていますので、ここでは重要な式です。
さて、上記の分圧回路で入力端子-GND間に接続されている抵抗![]() にかかっている電圧
にかかっている電圧![]() を求めます。
を求めます。
この場合は![]() がデジタルデータになっているだけですから、下式になります。
がデジタルデータになっているだけですから、下式になります。
![]()
基準電圧![]() が
が![]() 等分されていて、データがどのレベルにあるか(
等分されていて、データがどのレベルにあるか(![]() )で読み取った電圧が分かるわけです。
)で読み取った電圧が分かるわけです。
例
例えばデジタルデータ![]() が"800"である場合、以下のように代入できますので、値が求まります。
が"800"である場合、以下のように代入できますので、値が求まります。
![]()
抵抗にかかっている電圧![]() は約3.9Vということがわかります。
は約3.9Vということがわかります。
このとき、値を格納する変数は丸められないようにfloat型などにしておきましょう。
抵抗値(Rx)を求める
導出
測定回路にあるように測定抵抗![]() はGNDと入力端子の間に接続して測定します。
はGNDと入力端子の間に接続して測定します。
別に![]() を
を![]() と入力端子の間でもいいんですけど、私はGNDに接続する方が多いかもしれません。
と入力端子の間でもいいんですけど、私はGNDに接続する方が多いかもしれません。
サーミスタはこれで抵抗値を求めてから、温度を計算します。
入力電圧![]() は電源電圧(5Vや3.3V)にする場合もよくあります。
は電源電圧(5Vや3.3V)にする場合もよくあります。
分圧回路でとりあえず前述の式で電圧値として取得し、その後に抵抗を計算します。
この場合、抵抗![]() は既知でなければなりません。
は既知でなければなりません。
分圧の公式を今回の変数に当てはめると、下式になります。
![]()
分圧の公式の導出は省略します。
これを変形して![]() の式にします。
の式にします。
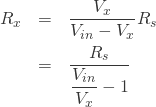
ここで、![]() ですから、これを代入すると下式のように変形できます。(前項で導出しました)
ですから、これを代入すると下式のように変形できます。(前項で導出しました)
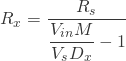
少しややこしいですが、これで抵抗値![]() が求まります。
が求まります。
![]() は定数ですから、あらかじめ計算しておいて求める際に
は定数ですから、あらかじめ計算しておいて求める際に![]() で割れば、計算量を少なくできます。
で割れば、計算量を少なくできます。
さらに![]() であれば、もう少しまとまります。
であれば、もう少しまとまります。
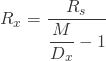
入力電圧![]() に5Vなどの電源電圧がかかっていて、それが基準電圧
に5Vなどの電源電圧がかかっていて、それが基準電圧![]() と同じというのはよくある状況です。
と同じというのはよくある状況です。
例
先ほどと同じくデジタルデータ![]() が"800"で、基準抵抗
が"800"で、基準抵抗![]() が1kΩであれば以下のように代入できますので、値が求まります。
が1kΩであれば以下のように代入できますので、値が求まります。
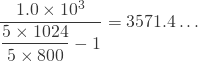
というわけで約3.6kΩと求まりました。
Rxが固定でRsの値を求める場合
逆に![]() が固定で
が固定で![]() の値を求めるとどうなるでしょうか。
の値を求めるとどうなるでしょうか。
別に難しいことはなく、先ほど導出した式を変形するだけです。
スポンサーリンク
![]()
あくまで、![]() は今回は固定値です。
は今回は固定値です。
![]() の場合も一応導出しておきます。
の場合も一応導出しておきます。
![]()
入力電圧(Vin)を求める
導出
ADCの最大入力電圧より高い電圧を測定したい場合は、分圧して電圧を下げてADCに入力します。
そして計算で分圧前の電圧(ここでは入力電圧)を求めますので、このような状況もよくあります。
ただしこの場合は![]() は固定値です。
は固定値です。
今回も分圧の公式を変形して![]() の式にします。
の式にします。
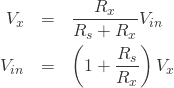
ここで、![]() ですから、これを代入すると下式のように変形できます。
ですから、これを代入すると下式のように変形できます。
![]()
これで![]() の値が求まりますね。
の値が求まりますね。
![]() は定数ですから、事前計算で計算量はかなり少なくできます。
は定数ですから、事前計算で計算量はかなり少なくできます。
例
同じくデジタルデータ![]() が"800"のとき、基準抵抗
が"800"のとき、基準抵抗![]() が2.2kΩで、固定抵抗
が2.2kΩで、固定抵抗![]() が1kΩであれば以下のように代入できますので、値が求まります。
が1kΩであれば以下のように代入できますので、値が求まります。
![]()
ということで入力電圧![]() は約13Vと求まりました。
は約13Vと求まりました。
ここで求めた式を実際に使うと、ピッタリ合う!と思いきやそうではありません。
いろんな要因があって、計算値と実際の値は異なります。
基準抵抗の誤差、配線の抵抗、入力電圧の精度など要因は様々です。
どうやって理想の値に近づけるかはまた別の話になってしまいますので、それはまた別の機会に。
スポンサーリンク









Leave a Comment