平均値などの逐次計算アルゴリズム

データの平均値をとることは多いですが、データが逐次的に入ってくるときは普通の計算では今までの全てデータが必要で総和を取る必要があり、これは計算量が多いです。
マイコンなどのメモリが少なく、スペックがあまり高くないシステムであれば、想像以上に影響が出てきます。
ここでは短い計算時間でメモリを節約でき、流れてくるデータの平均値を順次求めていく方法を紹介します。

平均値

よくある平均値の計算

平均値は10個のデータがあったとすると、その10個のデータをすべて足して、その総数である10個で割ればいいです。
上の文章で10をにすると平均値は下式となります。

   

プログラム例

この平均値の式で計算するプログラムで書くと下記のようになるでしょうか。

for (i = 0;i < total_num;i++) {
  sum += data[i];
}
average = sum / total_num;
total_num++;

このプログラムがループする感じだと思ってもらえればいいです。
sumは総和、data配列には逐次的にデータが入ってきて、それを総数total_numで割ります。
total_numはデータ数が増えるときにインクリメントしておきます。

この式で計算するとデータはどんどん増えていきますので、は増えていきます。
が小さければ計算量も同様に小さいですが、が1000や10000になるだけでも処理が大変なのが明らかです。

平均値の逐次計算

そこで平均値を逐次計算します。
これは平均値をどうやって求めるかという問題です。

   

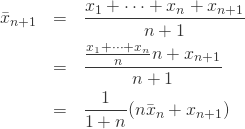
この変形は感心してしまいます。

上の式であれば、前までの平均値とその総数のデータさえあれば計算できます。
はどんどん増えていきますが、これは仕方ありません。
ずっとデータが増えていくわけですから。
データが多い場合はオーバーフローの可能性がありますね。
を増やしたくない場合は移動平均で処理するのが良いでしょう。

別の考え方として次のような式にも変形できます。

   

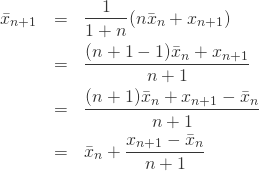
上式ではそれまでの平均値に、取得した値との微分（前進差分）を足すような形になりました。
どちらでやっても結果は同じですがこれはこれで面白いですね。

プログラム例

逐次計算できる式で平均値を求めるプログラムは下記のような感じでしょうか。

average = (total_num * average + data) / (total_num + 1);
total_num++;

かなりシンプルですね、平均値の計算は実質１行です。
配列が不要というのはメモリの使用量も少なく安心です。
ループ計算が無いので計算量はかなり少なそうです。

単純移動平均

普通の計算方法

平均値はすべてのデータを足し合わせるというものですが、移動平均は一定区間ごとの平均値という説明が簡潔でしょうか。
新しいデータが来たら、古いデータは捨ててまた平均を取ります。
10個のデータが最初にあったとして、11個目の新しいデータが来たら一番古い1個目のデータは捨てて2～11個目のデータを10で割ります。
平均値のようには増えませんね。

これを式で表すと、下式のようになります。

   

毎回個の総和を求める必要があるので普通の平均値を求めるよりは増え続けない分ましですが、それでも回ループを繰り返すのは結構な計算量にはなるでしょう。

単純移動平均の逐次計算

新しいデータを加えて、一番古いデータを除けばいいので、総和を求め直す必要はありません。
つまり計算量が少なく済みますね。
さらにも増えないので計算は単純です。

   

プログラム例

「一番古いデータ」というのが分からないといけませんので、配列などにデータ列を持っておく必要があります。
そして、配列をずらして一番古いデータを捨てて、新しいデータを入れなければいけません。
よくある配列をずらす方法はループ処理をします。
ただこれは避けたいので、できるだけ配列をずらす処理を軽くする必要があります。

上の記事でいろいろ苦労して考えましが、コメントで非常に良いアルゴリズムを教えていただきました。

if (cnt == TOTAL_NUM) cnt = 0;

sum -= data[cnt];
data[cnt] = value;
sum += data[cnt];
cnt++;

average = sum / TOTAL_NUM;

指数移動平均

指数移動平均はデータに重みをもたせます。
その重みは指数関数的に減少させます。

実はこの指数移動平均は結果から言えば、以前投稿したディジタルフィルタの記事のRCフィルタと一致します。
結局のところ移動平均はフィルタなんですね。
こういうところにつながってくるのは面白いです。

ですので、ここでは説明を省略します。

---

平均値を求める際は、紹介した方法で計算してみてください。
処理が軽くなるのでおすすめです。