
家庭のコンセントから取れる電源は交流ですが、実効値や電力を求めるのは結構ややこしいです。
電気回路を学び始めて最初の壁でしょうか。
では、実際に取得したデータから実効値や電力を求めるにはどうしたらいいでしょうか。
ここではそれらの値はどのようにして求めたらいいかまとめてみます。
正弦波だけでなく歪んでいたり、はたまた方形波だったり全然違う波形でも特性値を求める一般的な話をしたいと思います。
スポンサーリンク
事前準備
解説する前に変数を提示しておきます。
基本的には下の図のとおりです。
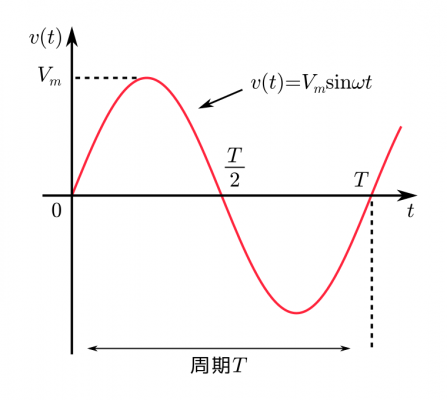
図は正弦波ですが、正弦波以外でも周期![]() や最大値
や最大値![]() は変わりません。
は変わりません。
電流の場合の関数は![]() みたいな感じで
みたいな感じで![]() や
や![]() を使います。
を使います。
また、ADCで取得した電圧のデータ配列を![]() 、電流のデータ配列を
、電流のデータ配列を![]() とします。
とします。
これらはADCで量子化されていますので離散値です。
今回はこれらの値をマイコン等で計算して、デジタルデータとして取得できている前提とします。
余談ですが、電圧や電流のデータを取得するのは大変です。
通常のADCはAC100V(最大約141V)なんて測定することは出来ません。
さらに負の電圧を測定することも出来ませんから、複雑な測定回路が必要です。
ADCにかかる電圧を下げるには分圧する必要がありますし、分圧するとそこから元の電圧を求め直す必要があります。
抵抗分圧回路での様々な値の求め方については別記事で紹介していますので、ご参考ください。
電流はシャント抵抗を使ったり、CT(カレントトランス)を使ったり、こちらも回路が複雑です。
このあたりは別の機会に...
平均値
交流(正弦波)の平均値は普通に平均を取ってしまうと0になってしまいます。
プラスとマイナスで打ち消し合うからですね。
そこで賢い人達が考えた平均値![]() の定義式は以下のとおりです。
の定義式は以下のとおりです。
![]()
簡単に言うと絶対値を取って平均すればいいんです。
ただしこれは連続している場合ですので、ここから取得したデータ![]() の配列で求めるには以下のようにします。
の配列で求めるには以下のようにします。
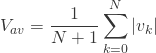
積分は使えないので総和で計算します。
![]() はデータの数ですが、
はデータの数ですが、![]() で割っているのは
で割っているのは![]() だと1個増えるからですね。
だと1個増えるからですね。
サンプリングしたすべてのデータの総和を求めるのは大変ですので、移動平均を使ったりして工夫します。
このあたりのアルゴリズムに関しては今回説明しませんので、別記事を参考にしてください。
平均を取るのはいいですが、交流の場合はサンプリング周期を気にしないとおかしなデータになってしまいます。
周期的な波形でもタイミングによって取得する値が変わってしまいますから。
正弦波交流での平均値
![]() が正弦波交流だとすると
が正弦波交流だとすると![]() です。
です。
先の平均値の定義式に代入して計算すると以下のように求まります。
![]()
だとすればmax関数とかで最大値を取ってさえいれば平均値が求まることになります。
といっても最大値を使って平均値を求めることははあまりやらないかもしれません。
最大値と言ってもばらつきは絶対にあります。
最大値を求めてそこで平均を取る必要があるなら、最初から平均を求めたほうが楽じゃないですか?
あと、平均値自体を使うことも少ないかと思います。
実効値のほうが実用性が高いですので...
実効値
実効値は定義はRMS、2乗して 平均した値の 平方根(root mean square)です。
これを![]() に当てはめれば実効値
に当てはめれば実効値![]() は以下のようになります。
は以下のようになります。
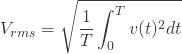
これを求めるのは結構大変です。
離散値にしても結局やってることは変わりません。
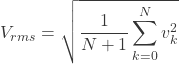
正弦波交流での実効値
上記の計算は複雑なので、コストが掛かります。
商用電源に使われている正弦波に限った計算をすると非常に簡単に求めることができます。
ご存知かもしれませんが、最大値のルート2分の1倍すればいいのです。
![]()
こうすれば平均と同様に最大値を取ってルート2分の1倍すれば実効値です。
また、正弦波に限った話をしますと平均値![]() から求めることができます。
から求めることができます。
![]()
Tips:真の実効値とは
高いテスターでは「真の実効値表示」というのがあると思います。
安いテスターでは実効値を表示してくれないのかといえば、そういう場合もあるという回答になります。
前項の『実効値』で説明した通りなのですが、定義と同じに実効値を求めるとコストが掛かります。
ですので安いテスターは正弦波を測定すると割り切って平均値の定数倍(![]() 倍)して計算しています。
倍)して計算しています。
これを平均値整流形といいます。
平均値整流形は測定信号が正弦波という前提で計算されますので、測定信号が方形波だったり三角波だと正しくない値が表示されます。
真の実効値表示機能がある場合は定義通りに計算していますので、測定信号がどのような波形であっても正しい値が表示されます。
皮相電力
正弦波交流での皮相電力![]() は電圧の実効値
は電圧の実効値![]() と電流の実効値
と電流の実効値![]() の積です。
の積です。
![]()
前項までで実効値は計算できますので簡単です。
有効電力
有効電力は皮相電力に力率を掛ければいい、そう思うかもしれません。
でもどうすれば力率![]() の位相差
の位相差![]() を求められるのでしょうか?
を求められるのでしょうか?
力率計を使いますか?それは余分なコストが掛かってしまいます。
正弦波ならなんとか位相差を求められるかもしれません。
ただし非線形波形ならそれは難しいです。
スポンサーリンク
そこで有効電力![]() の定義式を振り返って見てみます。
の定義式を振り返って見てみます。
![]()
有効電力は瞬時電力の平均なんです。
離散値で求めるには積分を総和にするだけでいいので下記のようになります。
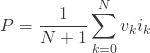
無効電力
前項までで「皮相電力」と「有効電力」が分かっていますので、無効電力は簡単に求まります。
皮相電力![]() と有効電力
と有効電力![]() 、無効電力
、無効電力![]() の関係式は
の関係式は![]() ですのでこれを
ですのでこれを![]() の式に変形します。
の式に変形します。
![]()
これで簡単に求まりますね。
力率
こちらも前項までで「皮相電力」と「有効電力」が分かっていますので、簡単に求まります。
「有効電力」のところで書いたように有効電力は皮相電力に力率を掛ければいいですからこれを式にすると以下のようになります。
![]()
これを![]() の式にします。
の式にします。
![]()
有効電力![]() を皮相電力
を皮相電力![]() で割ればいいだけです。
で割ればいいだけです。
位相差
力率![]() は
は![]() ということが分かっていますので簡単です。
ということが分かっていますので簡単です。
逆三角関数で求められますね。
![]()
個人的に使う場面があったのでまとめてみました。
備忘録的な感じですが、振り返ってみて「なるほど」となったところもあります。
たまに復習してみると、それはそれで面白いかもしれませんね。
スポンサーリンク






Leave a Comment